

- 尺規作圖............................................. 多一點有甚麼關係?尺規作圖三大問題的早期歷史
- 連分數..................................................日蝕預測
- 解題策略 1.極端化原理 2.簡單化原理 3.轉化原理 4.類比原理 5.建立座標系
- 數學歸納法
- 柯西不等式 (1)廣義的柯西不等式
(2)廣義的閔可夫斯基不等式
(3)柯西不等式的推廣
(4)柯西不等式及其證明(Young不等式)Holder不等式
(5)各種不等式
[Inequalities] by Hardy-Littlewood-Polya
- 疊合原理................................................一般解=齊次解+特別解
- 數學期望值..........................................品茶師必須答對幾杯? [L13]
- 類比..................................................... 中國餘數定理與Lagrange插值法。[L14]
- 反射定律..............................................尺規作圖與Galois理論。[完美出桿]
[L16]
- 鴿籠原理..............................................聖經密碼不能說的秘密? [鴿籠原理.html]
[L17]
- 行列式二三事......................................Cramer公式的幾何意義。[L19]
- 一題多解..............................................開放性思考與邏輯訓練。(讀者的指正與迴響) ;一道數學競賽題的九種解法
[L20]
- 不變量與尋找動點的軌跡方程式......諸法生滅與不生不滅。[L21]
- 數學課程中的兩個邏輯概念..............沒有邏輯的數學是盲目的 沒有數學的邏輯是空洞的。[L22]
- 曲線族與包絡線..................................噴泉隨著重金屬的樂音揮灑,水柱構成完美的包絡面。[L23]
- 等周長定理..........................................."聽音辨位是修練暗器的功夫,聽音辨形>".....。 [等周長不等式] [L
24]
- C60.........................................................球面的Euler特徵數=2。分子拓撲學的出現。
[L25]
- 遞迴數列...............................................不動點解法:製造新數列是個不錯的想法。多項式除法與遞迴數列
[L26]
- 不動點理論(關於分式型遞迴數列的不動點解法)
[L42]
- 無窮調和級數 疊書問題
[L27]
- 模式(pattern)的迷思..............................一個美麗的錯誤。[L28]
- 相關係數...............................................為什麼老師不支持這個科學方法?[L29]
- 丟番圖(Diophantus)方程式
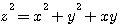 的一般解。[L30]
的一般解。[L30]
- 費氏數列................................................費氏數列空間的疊合原理。
- 芝諾(Zeno)詭論.....................................色即是空,空即是色。
- 等權三鎮(Steiner問題)...........................
- 蜂巢結構........................................... ...1.蜜蜂跳舞 ( Karl Ritter von Frisch) 2.蜂舞。
- 史都華先生(Ian Stewart 1945~ )提倡一種新的數學:形態數學(morphomatics)
- 數形合一..............................................從畢達哥拉斯到52屆中學數學科展。
[平面嵌鋪] [相似形]
- 阿波羅圓
- 整係數一次因式檢驗法(牛頓定理) 高斯引理
- 邏輯發展史 哥德爾定理
- 古埃及分數 為什麼古希臘有這麼多數學家
- 病毒的傳播模型
- 訊息 密碼
- 3D 幾何
- 投影的面積
- 轎車與山羊 貝氏定理
- 克普勒猜想(Johannes Kepler 1571~1630) 1611: 面心立方堆積是所有堆積中最密的
Maryna
Viazovska 8維空間的球堆積
- 龍騰數亦優雜誌
[L]
![]()