中國現存最早的數學典籍為"周髀算經",九章算術才真正是第一部把古代中國數學已有的知識加以總結的書籍。
劉徽(約225~295)註 用割圓術算出圓周率~3.1416
南北朝時人祖沖之(429~500)是偉大的數學家 天文學家 ,把pi的近似值又向前推了一步
把九章算術推得最遠的是吳文俊先生(1919~2017)---數學機械化
......
祖沖之的兒子祖暅也是數學家
祖暅原理記載在"九章算術"卷4,"少廣"---開立圓術,李淳風註,原文是"羃勢既同,則積不容異"。
西方稱卡瓦列里(Caralieri 1598~1647)原理
是用來求體積的 它的原理也適用於求面積 請看胖子原理
(在等周長定理的習作第4題 有根據史坦那(Jocob Steiner 1796~1863)對稱化法求橢圓的面積 用的也是祖暅原理)
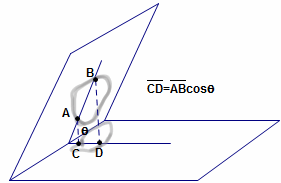
平面E與平面F夾角=
S是平面E上圖形的面積,它在平面F的投影面積=T,則T=Scos
S上每一個線段AB在平面F的投影CD=ABcos,由胖子原理T=Scos,得證
例如
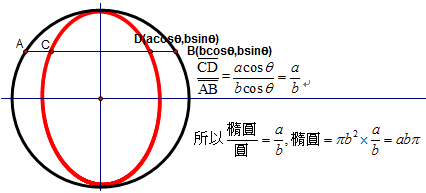
你想像一下 這些面積是許多細微線段累積成的面積 就可以想像裡面有德謨克利特原子論的影子
體積也是一樣
所以 德謨克利特可以推出錐體體積的公式 阿基米德可以算出y=x^2在x=0~1下的面積是1/3
極限的觀念是變動的概念 則非常難纏 所以數學發展史上 微積分 先有積分 後有微分
而發現(看出)微分與積分的關係 就需要慧眼 是牛頓與萊布尼茲幾乎同時發現的 在水到渠成之際
因為很重要 所以稱為微積分"基本"定理 最後就一路推廣到Stoke定理了
......
為何球的表面積是它影子的4倍
[球的體積] [圓的面積]......
以下是跟投影面積有關的另一件事
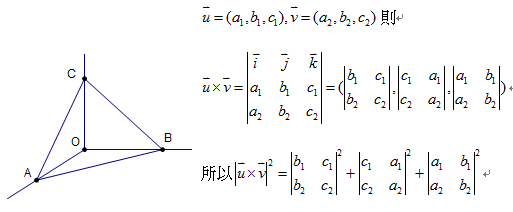
即
這就是畢氏定理的推廣 從一維推廣到二維
我高中時 從向量式發現畢氏定理的推廣 高興了一下子 然後終身難忘
它沒有甚麼價值 就像一棵樹 偶而可以在樹下乘涼一下 如此而已
但是 仔細想一想 人生不就是這樣而已嗎