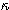Ricci flow and Poincare conjecture   by John Morgan 、Gang Tian(田剛 1958~)

 Introduction

Part I        Background from Riemannian Geometry and Ricci flow

Chapter 1. Preliminaries from Riemannian geometry

Riemannian metrics

Levi-Civita connection

Hess(f)

Curvature   (Curvature2)Bianchi identity Uniformization Theorem

Geodesics

Exponential map

Hopf-Rinow theorem

Jacobi fields

Gaussian normal coordinates

comparison theorem

 cone

 

Chapter 2. Manifold of non-negative curvature

Chapter 3. Basics of Ricci flow                            何謂孤立子(Soliton) 

Chapter 4. The maximum principle

Chapter 5. Covergence results for Ricci flow

Part II Perelman's length function and its applications

Chapter 6. A comparison geometry approach to the Ricci flow

Chapter 7. Complete Ricci flows of bounded curvature

Chapter 8. Non-collapsed results

Chapter 9. 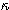-non-collapsed ancient solutions

Chapter 10. Bounded curvature at bounded distance

Chapter 11. Geometric limits of generalized Ricci flow

Chapter 12. The standard soluton

Part III Ricci flow with surgery

Chapter 13. Surgery on a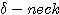

Chapter 14. Ricci flow with surgery : the difinition

Chapter 15. Controlled Ricci flow with surgery

Chapter 16. Proof of the non-collapsing

Chapter 17. Completion of the proof of Theorem 15.9

Part IV Completion of the proof of the Poincare Conjecture

Chapter 18. Finite-time extinction

Chapter 19. Completion of the proof Proposition 18.24