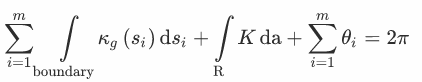Gauss-Bonnet定理

 

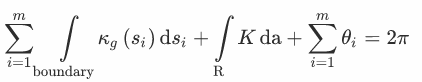
§ 01

古典的證明------D J.Struik    

從holonomy角出發的證明------微分幾何講稿  大域微分幾何 by 黃武雄

§ 02

  1. 取么速測地座標系 E=1,F=0 ,得
  2. 曲面上向量場Z沿一曲線方向的共變微分 平行移動
  3. 切線轉角定理  
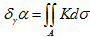
  4. 曲線的切向量T
    然後證明

§ 03 應用

  1. 一個正曲率的緊緻(compact)曲面與球面同胚
  2. 毛球定理
  3. Hopf-Poincare標數定理
  4. Jacobi定理
  5. T是一個測地線三角形 則其三內角和(1)= 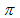K=0 (2)> 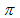K>0 (3)< 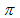K<0
[Lecture 27]