 V.I.Arnold 1937~2010
V.I.Arnold 1937~2010
- Ordinary Differential Equations
- Lectures on Partial Differential Equations
- Mathematical Methods of Classical Mechanics
- Catastrophe Thoery
- Symplectic Geometry and Topology
- Mathematical Understanding of Nature
- Memories of Arnold
Abel's Theorem in Problems And Solutions: Based on the lecture of Professor V.I.Arnold
Geometrical Methods in the Theory of Odinary Differential Equations
第一章 基本概念
- Phase Spaces
- Vector Fields on the Line
- Linear Equations
- Phase Flows
- The Action of Diffeomorphism on Vector Fields and Direction Fields
- Symmetries
- Conservative fields
Bernoulli equation 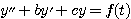
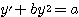 Power series
Power series
第二章 基本定理
- Rectification Theorems
- Applications to Equations of Higher Order
- The Phase Curves of an Autonomous System
- The Derivative n the Direction of a Vector Field and First Integrals
- First-Order Linear and Quasi-linear Partial Differential Equations
- the Conservative System with one Degree of Freedem
第三章 線性系統
- Linear Problems
- The Exponential Function
- Properties of The Exponential
- The Determinant of an Exponential
- Practical Computation of The Matrix of an Exponential
- Complexification and Realification
- ...
- Linear Systems
- The Laplace transform
第四章 Proofs of The Main Theorems
第五章 Differential Equations on Manifolds
- Differential Manifolds
- The Tangent Bundle Vector Fields on a Manifold
- The Phase Flow defined by a Vector Field
- The Indices of the Singular Points of a vector Field
Examination Topics Sample Examination Problems Supplementary Problems
 V.I.Arnold 1937~2010
V.I.Arnold 1937~2010
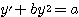 Power series
Power series