Paul Erds 1913~1996

Paul Erdos是本世紀最偉大的數學家之一,也是性情最古怪的一位。終身未婚,沒有家庭,固定住所,固定職業,一生大多以演講費,獎金,借貸過活,但是又散盡所得幫助年輕的數學家。發表過1500多份論文,書籍與文章,產量堪與Euler相比,部分作品更成為21世紀的偉大經典;並且開創了合作寫論文的風氣,一生合作過的數學家超過450人。

他出生在匈牙利首都,布達佩斯...一個用孕育無數偉大心靈的地方。直到21歲,因為納粹迫害猶太人而離開,到世界各地漂泊。

這本書"不只一點瘋狂...天才數學家艾狄胥"。原作者是Bruce Schechter,曾蕙蘭翻譯,由先覺出版社發行。看完本書保證你能感染到數學家對數學的狂熱,與對生命意義的執著...生命的意義在於猜想與證明,Erd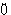s如是說。

讀完本書,很高興的是

  1. Erdos也喜歡下圍棋 。
  2. 可以用Ramsey定理解釋"聖經密碼",破除我前一陣子的迷思 。 
  3. 除了John von Neumann,George Soros(1930--),George Polya外又找到一個"火星人"。 
  4. 更高興的是沒多久看到建國中學設立中學通訊解題。

1930年代布達佩斯的咖啡屋孕育了無數高手,希望我們嚮往之餘,停步思考一下,我們知識的殿堂在那裡?

本書所穿插的數學內容略加整理:

(1)質數:

  1. 質數的個數有無限多個 p.066
  2. Eratosthenes篩法     p.186
  3. 兩連續質數之間的最大距離為何?              p.068
  4. 1~2n的正整數中,取相異n+1個,則必有兩數互質  p.237
  5. 1~2n的正整數中,取相異n+1個,則必有一數為另一數的因數
  6. n>1,則n與2n之間必有一質數(Chebyshev定理) p.076
  7. Mersenne 質數 p.064 數學傳播季刊第21卷第3期p.14(GIMPS)
  8. 質數定理(prime number theorem p.185~208 )所引起的江湖恩怨

(2)正方形的分割(dissection p.125~128)

(3)Goldbach 猜測 p.213:

(4)Ramsey定理:( p.101~119)是鴿籠原理的推廣,如何解釋"聖經密碼",火星西多尼(Cydonian)平原的人猿面孔,以及夜空星座?它的意義是:不可能完全無序。

  1. 平面上5點,任3點不共線 ,則其中有4點會形成凸4邊形. p.101
  2. 宴會問題 R(3,3)=6,R(4,4)=18,R(5,5)=? 

(5)機率 p.144:某電視節目,三個門後,其中一個門後有一輛轎車,另兩個門後各有一隻山羊, 你先選一個門,然後主持人打開另一個門,               發現是一隻山羊,主持人問你要不要換?你覺得換有利或者換不換都是一樣?   科學月刊1998/11 p.906轎車與山羊

  1. 數學傳播季刊21卷3期 p.63 棋盤染色問題與二部Ramsey數
  2. 數學傳播季刊21卷4期 p.4
  3. Erdos Number Project
  4. 一條畫不清的界線(李國偉) p.82

[解答1]

n!+2,n!+3,...n!+n都不是質數,for n>2,所以兩連續質數的距離可以是無限大

[解答2]因為一定會取到兩相鄰整數

[解答3]

1~2n之間取n+1個數 a1,a2,a3,…,an+1, 把2的因數去掉,例如:6=2x3--->3,8=23x1--->1 得到1~n之間的n+1個奇數b1,b2,b3,…,bn+1 由鴿籠原理,存在i<j使得bi=bj 但是ai=2pxbi,aj=2qxbj,所以ai與aj有因數倍數的關係

[註1]

  1. 高斯經由大量的計算結果,推測出質數分布的情形
  2. J. Hadamard與C.J. de la Vallee Poussin運用複變函數分別證明質數定理
  3. N. Wiener 1930年
  4. Paul Erdos ,A.Selberg完成初等證明
  5. N, Levinson 1960年代在"美國數學月刊",刊出幾頁幾乎不能再簡單的證明
  6. 數學傳播季刊第10卷第1期 p.98質數的分布