[積分因子---李群的觀點][可積的動力系統]似乎是Frobenius定理的延續

Frobenius定理從(偏)微分方程 向量場 Differential form 到幾何力學 輪郭慢慢呈現

可以確定的是 不管是李群還是Frobenius定理 (偏)微分方程都是源頭

據稱 Sophus Lie發展李群的初衷是為了要尋求一個解(偏)微分方程一個系統性的方法

所以 微分幾何與(偏)微分方程是一枝兩葉 必須同時掌握

不能用尺規作圖把60度三等分 昨天聽T跟學生這麼說

這個問題高中生可以懂一些 國中生只能聽聽

尺規作圖是古希臘的重要課題 當然延續到Galois理論 三大問題要用現代代數(群論)解決

兩千多年 夠久遠吧

/...

如果你看到一些真正棘手複雜的論證, 那麼有兩種可能, 要嘛作者並不真正明白他在說什麼, 要嘛論證是錯誤的。

因為如果是經過真正理解的論證, 應該是簡單的。Mikhael Gromov如是說

[結 分子 宇宙]

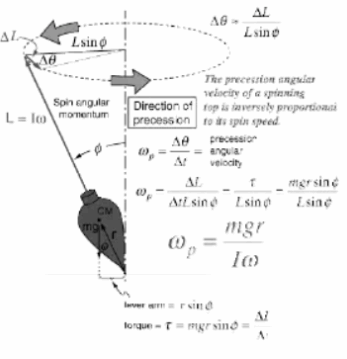
有時候 生活就像陀螺 有自轉也有公轉的部份

昨天到台南 廣澤整體 因為T妹的坐姿不良需要調整 來回要兩小時 家人就是要互相照應

有時候 生活就是一個結 剪不斷 理還亂 書 東看西看 不太能整理出頭緒

早上 靜坐片刻 想一想 生命留給自己的時間 好像很多 又好像不多

何時才能覺醒

[傅科與Levi-Civita]這是張海潮先生一篇簡短有趣的文章 對Levi-Civita的平行移動有精要說明 並且以傅科擺為例

文章最後 海潮先生說 Levi-Civita會受到傅科的啟發嗎

也許Levi-Civita寫的這本書[The Absolute Differential Calculus]會有答案

鏡像之美 很美 很數學