天才之旅
作者:William Dunham.林傑斌先生翻譯,余文卿先生審定(牛頓出版社)
這是一本為一般大眾所寫的數學史的書,談論數學史上偉大定理的重要所在-----其洞察力與創造性,以及數學家解決問題的方法。
每章後面的結語對定理的來龍去脈多有俾益。適合中學教師或對數學蠻有興趣的高中學生課外閱讀,需要細細品嚐。
- Hippocrates的新月形平方法
- 從尺規作圖到為什麼"化圓為方"是不可能的(Ferdinand
Lindermann 1882) p.28
- 歐幾里德(Euclid)對畢氏定理的證明(約西元前300年)
- 歐幾里德對演繹法的重視,使得"幾何原本"歷經2000年仍然歷久彌新
- "三角形任兩邊和大於第三邊"(命題20)是一個非常顯然的事實,為什麼還要證明?p.47
- 如何巧妙地證明畢氏定理p.54
- 由公設(5)到非歐幾何的簡史
- 歐幾里德(Euclid)與質數無窮論
- 第一個完全數(perfect number)是6=1+2+3,第二個是28,...
若1+2+4+...+2n是質數,則N=2n(1+2+...+2n)是一個完全數
這樣的質數叫作梅仙尼質數(Mersenne
primes) p.86
有沒有奇完全數是一個open problem
- 歸繆證法的第一個應用:質數有無窮多個 。
- 正多面體(regular solids)p.90有五種:(及其證明)
- Archimedes(287~212B.C.)求圓的面積
- 阿基米德是裸奔的始祖 。
- 有人說,歷史上最偉大的物理學家是:1.阿基米德 2.牛頓 3.愛因斯坦 4.楊振寧
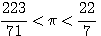 最偉大的鉅作:論球體與圓柱體p.15
最偉大的鉅作:論球體與圓柱體p.15 - 你知道球面積與體積的關係嗎?
 的簡史p.120
的簡史p.120
- Heron的三角形面積公式
- Eratosthenes( 284~192B.C.):
1.關於質數的篩法(sievs
method)
2.對地球周長的測定-------宇宙的詩篇 - Apollonius (262~190 B.C.):
圓錐曲線論 - Heron:
1.Dioptra----解釋挖掘山洞與測量泉水流量
。
2.Metrica(測量術)----你想知道三角形面積公式的古典證法嗎?
EX:從Heron公式證明畢氏定理 p.145
- 從西元641年到1085年阿拉伯人是希臘文明的守護神,歐洲在文藝復興時甦醒過來
。
- Cardano與三次方程式的解
- 三次方程式的公式解的故事當然要一直說到Galois的群論為止
。
- 我最近遇到好幾個"不可能"的定理:
1.一元5次方程式沒有公式解
2.不完全定理
3.不存在判定一個Diophine方程式有沒有整數解的算法(algorithm)(Hilbert第10問題)
還有什麼"不可能"的事?!
- Newton(1642~1727)的寶石
- 二項式定理(binomial theorem)(1665年)
- 分析學(1669年)
- 自然哲學的數學原理(1687年)
- 光學(1704年)
- Bernoulli兄弟與調和級數
- Euler奇特的求和方法
- Euler的數論
- 連續統的不可數性質
- Cantor與超限王國
後記:
- 我一直以為:"三角形任兩邊和大於第三邊"的證明是直接由公設(1)("由任意點到任意點可作一直線") 得到,看了本書才恍然大悟 。真是愧對歐幾里德了 。
- 外國人名還是應該都註明英文,例如歐都克斯 p.32
 數學傳播季刊第20卷第1期---余文卿:談"天才之旅"
數學傳播季刊第20卷第1期---余文卿:談"天才之旅"
 歐幾里得 幾何原本(九章出版社 )
歐幾里得 幾何原本(九章出版社 )
 Download
Download
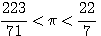 最偉大的鉅作:論球體與圓柱體p.15
最偉大的鉅作:論球體與圓柱體p.15  的簡史p.120
的簡史p.120